奇函數關於什麼對稱 奇函數的定義

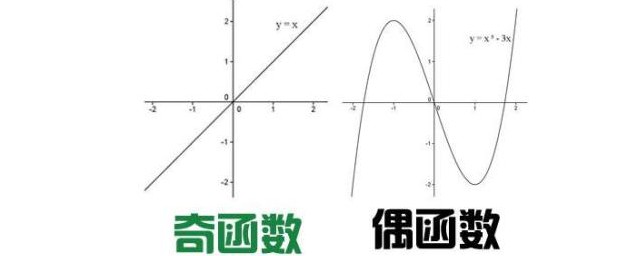
1、奇函數圖象關於原點對稱。

2、奇函數的定義域必須關於原點對稱，否則不能成為奇函數，若為奇函數，且在x=0處有意義。

3、設在定義域上可導，若在上為奇函數，則在上為偶函數，兩個奇函數相加所得的和或相減所得的差為奇函數。

4、一個偶函數與一個奇函數相加所得的和或相減所得的差為非奇非偶函數，兩個奇函數相乘所得的積或相除所得的商為偶函數，一個偶函數與一個奇函數相乘所得的積或相除所得的商為奇函數。

5、如果一個函數f(x)的定義域內的任何一個x和值域內的任何一個y，都有f(-x)=-f(x),且定義域也關於原點對稱的話就說f(x)為奇函數（就是說這個函數f(x)的任何一個點（X,Y）都有對稱點的話就稱其為奇函數）。